Operaciones con Conjuntos: Una Guía Completa
Exploraremos el concepto de conjuntos. Veremos su importancia en matemáticas y otras disciplinas. Descubriremos su aplicación en bases de datos, lógica.
DO
by DEYANIRA OR
¿Qué es un Conjunto?
Definición Formal
Un conjunto es una colección bien definida de objetos distintos.
Ejemplos
Conjuntos de números pares, vocales del alfabeto, etc.
Notación
A = {1, 2, 3, 4}, B = {a, e, i, o, u}.
Conjunto Vacío
El conjunto vacío (∅ o {}) no contiene elementos.

Representación de Conjuntos
1
Extensión
Listado explícito de todos los elementos: A = {2, 4, 6, 8}.
2
Comprensión
Definición mediante una propiedad: B = {x | x es un número par menor que 10}.
3
Diagramas de Venn
Representación gráfica mediante círculos dentro de un rectángulo.
Conjunto Universal y Subconjuntos
Conjunto Universal (U)
Contiene todos los elementos del tema.
Subconjunto (⊆)
A es subconjunto de B si todo elemento de A está en B. A = {1, 2}, B = {1, 2, 3}. A ⊆ B.
Subconjunto Propio (⊂)
A ⊆ B y A ≠ B.
Superconjunto (⊇)
B es superconjunto de A si A ⊆ B.

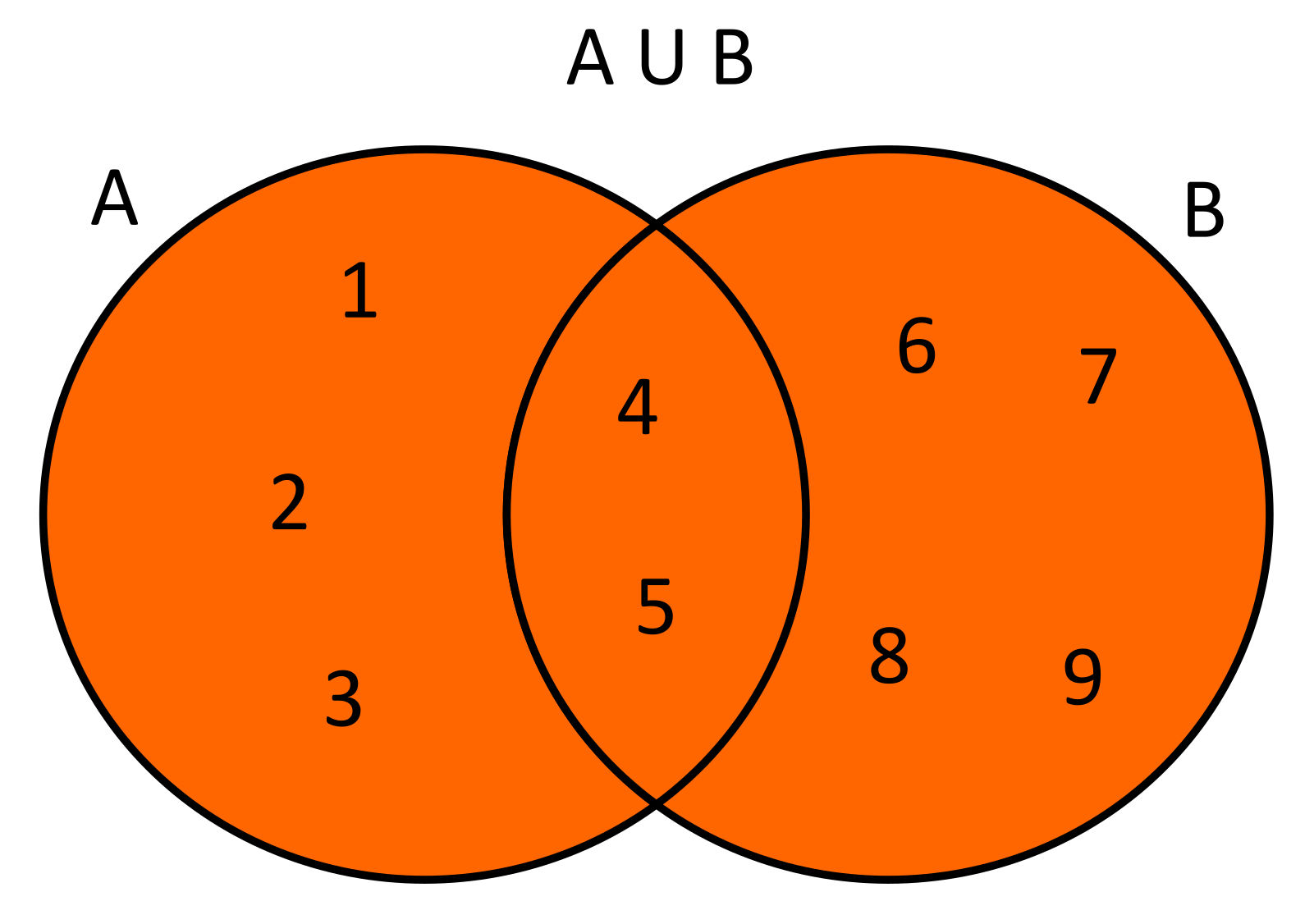
Unión de Conjuntos (∪)
1
Definición
A ∪ B = {x | x ∈ A o x ∈ B}.
2
Ejemplo
A = {1, 2, 3}, B = {3, 4, 5}. A ∪ B = {1, 2, 3, 4, 5}.
3
Diagrama de Venn
Representación visual de la unión.
Intersección de Conjuntos (∩)
Definición
La intersección de dos conjuntos A y B se define como el conjunto de todos los elementos que pertenecen tanto a A como a B. Formalmente, A ∩ B = {x | x ∈ A y x ∈ B}.
Ejemplo
Consideremos los conjuntos A = {1, 3} y B = {3, 4}. La intersección A ∩ B contendrá solo el elemento 3, ya que es el único que está presente en ambos conjuntos. Por lo tanto, A ∩ B = {3}.
Conjuntos Disjuntos
Dos conjuntos A y B se consideran disjuntos si no tienen elementos en común, es decir, su intersección es el conjunto vacío. En otras palabras, A ∩ B = ∅, lo que significa que no hay ningún elemento x tal que x ∈ A y x ∈ B simultáneamente.

Diferencia de Conjuntos (-)
1
Definición
A - B = {x | x ∈ A y x ∉ B}.
2
Ejemplo
A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8, 9}.
A - B = {1, 2, 3} (imagen). Pero B - A = {6, 7, 8, 9}.
3
Importante
A - B ≠ B - A.
Diferencia Simétrica de Conjuntos (A Δ B )
Definición
A Δ B = {x | x ∈ U y x ∉ ∩}.
Son todos los elementos de la unión PERO NO los de la intersección.
Ejemplo
A = {1, 2, 3, 4, 5}.
B = {1, 2, 6, 7}
A Δ B = {3, 4, 5, 6, 7}.


Complemento de un Conjunto (A')
Complemento de un Conjunto (A')
Definición:
A' ={x | x ∈ U y x ∉ A}. Ejemplo: U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 2, 9}. A' = {3, 4, 5, 6, 7, 8}.
Ejercicios Prácticos
Ejercicio 1: U = {a, b, c, d, e}, A = {a, b}, B = {b, c}.
Representar los conjuntos en diagramas de Venn.
Calcular A ∪ B, A ∩ B, A - B, B - A, A', B´, A Δ B.
Ejercicio 2: Encuesta sobre preferencias de deportes. A = {personas que prefieren fútbol}, B = {personas que prefieren baloncesto}. Interpretar A ∪ B, A ∩ B, A -B.
Conclusiones y Aplicaciones Futuras
1
Resumen de las operaciones con conjuntos.
2
Importancia en diversas áreas del conocimiento.
3
Temas avanzados: Aplicación en situaciones de la vida cotidiana como en la Empresa.
4
Invitación a explorar la guía de matemáticas que está en el blog.